杨氏模量的定义

设金属丝的原长为L，横截面积为S，沿长度方向施力F后，其长度改变ΔL，则金属丝单位面积上受到的垂直作用力σ=F/S称为正应力，金属丝的相对伸长量ε=ΔL/L称为线应变。实验结果指出，在弹性范围内，由胡克定律可知物体的正应力与线应变成正比，即：

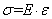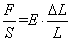（1）或（2）

比例系数E即为金属丝的杨氏模量（单位：Pa或N/m2），它表征材料本身的性质，E越大的材料，要使它发生一定的相对形变所需要的单位横截面积上的作用力也越大。

由式（2）可知：

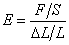（3）

对于直径为d的圆柱形金属丝，其杨氏模量为：

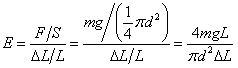（4）

式中L（金属丝原长）可由卷尺测量，d（金属丝直径）可用螺旋测微器测量，F（外力）可由实验中数字拉力计上显示的质量m求出，即F=mg（g为重力加速度），而ΔL是一个微小长度变化（mm级）。针对ΔL的测量方法，本实验仪采用光杠杆法。

光杠杆法

光杠杆法主要是利用平面反射镜转动，将微小角位移放大成较大的线位移后进行测量。仪器利用光杠杆组件实现放大测量功能。光杠杆组件包括：反射镜、与反射镜连动的动足、标尺等组成。其放大原理如图 1所示。

图 1  光杠杆放大原理图

开始时，望远镜对齐反射镜中心位置，反射镜法线与水平方向成一夹角，在望远镜中恰能看到标尺刻度x1的像。动足足尖放置在夹紧金属丝的夹头的表面上，当金属丝受力后，产生微小伸长ΔL，与反射镜连动的动足尖下降，从而带动反射镜转动相应的角度θ，根据光的反射定律可知，在出射光线（即进入望远镜的光线）不变的情况下，入射光线转动了2θ，此时望远镜中看到标尺刻度为x2。

实验中D>>ΔL，所以θ甚至2θ会很小。从图 1的几何关系中我们可以看出，2θ很小时有：

ΔL≈D∙θ，Δx≈H∙2θ

故有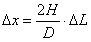：（5）

其中2H/D称作光杠杆的放大倍数，H是反射镜中心与标尺的垂直距离。仪器中H>>D，这样一来，便能把一微小位移ΔL放大成较大的容易测量的位移Δx。将式（5）代入式（4）得到：

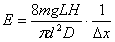（6）

如此，可以通过测量式（6）右边的各参量得到被测金属丝的杨氏模量，式（6）中各物理量的单位取国际单位（SI制）。